Vectors: Difference between revisions
No edit summary |
|||
| (17 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
'''Vectors''' are mathematical representations of any thing that has a length, or magnitude, and direction. | [[Category:Scripting Reference]] | ||
'''Vectors''' are mathematical representations of any thing that has a length, or magnitude, and direction. Positions are also described using vectors which start at the origin of the coordinate system (0,0,0). | |||
== Definition == | == Definition == | ||
In GraalScript, a vector is limited to three dimensions, however, mathematics allows for analyses of vectors in n-dimensions. Vectors do not have | In GraalScript, a vector is limited to three dimensions, however, mathematics allows for analyses of vectors in n-dimensions. Vectors do not have positions. Two vectors are said to be parallel if they have the same direction (u || v), and are said to be equal if they are parallel and have the same magnitude (u = v). Vectors are generally described by their terminal points with respect to the origin (0,0,0). | ||
The basic format of a vector in GraalScript is {x,y,z} where x, y, and z are all floating points in reference to the axis to which they correspond. Built into GraalScript are several functions which can be used to analyze these vectors. | The basic format of a vector in GraalScript is {x,y,z} where x, y, and z are all floating points in reference to the axis to which they correspond. Built into GraalScript are several functions which can be used to analyze these vectors. | ||
| Line 14: | Line 15: | ||
To denote the difference between a scalar and a vector, vectors are often written with a directional arrow above them, which looks like the top half of an arrow pointing right. In GraalScript, a scalar and a vector are impossible to confuse: a scalar is a floating point whereas a vector is a string. | To denote the difference between a scalar and a vector, vectors are often written with a directional arrow above them, which looks like the top half of an arrow pointing right. In GraalScript, a scalar and a vector are impossible to confuse: a scalar is a floating point whereas a vector is a string. | ||
=== Vector Length (Magnitude) === | === Vector Length (Magnitude/Modulus) === | ||
Being as vectors are merely written by terminal point coordinates, there is no immediate way to determine the magnitude of the vector. Mathematically, the terminal point lies on a sphere that has the same radius as the vector's magnitude. Thus, we can use the equation of a sphere to calculate the magnitude.<br /> | Being as vectors are merely written by terminal point coordinates, there is no immediate way to determine the magnitude of the vector. Mathematically, the terminal point lies on a sphere that has the same radius as the vector's magnitude. Thus, we can use the equation of a sphere to calculate the magnitude.<br /> | ||
r<sup>2</sup> = x<sup>2</sup> + y<sup>2</sup> + z<sup>2</sup><br /> | r<sup>2</sup> = x<sup>2</sup> + y<sup>2</sup> + z<sup>2</sup><br /> | ||
r = √(x<sup>2</sup> + y<sup>2</sup> + z<sup>2</sup>) | r = √(x<sup>2</sup> + y<sup>2</sup> + z<sup>2</sup>) | ||
where r is the magnitude. Generally, the magnitude is denoted as |v| or ||v||. This was chosen, because absolute value refers to distance from the origin, thus the marks were suitable. In GraalScript, however, the magnitude of any vector can be calculated simply by plugging a vector string into the '''vectorlen({{graycourier|v}})''' function. | where r is the magnitude. Generally, the magnitude is denoted as |v| or ||v||. This was chosen, because absolute value refers to distance from the origin, thus the marks were suitable. In GraalScript, however, the magnitude of any vector can be calculated simply by plugging a vector string into the '''vectorlen({{graycourier|v}})''' function. | ||
=== Unit Length === | |||
A vector is said to have "unit length" when it's magnitude is one. '''i''', '''j''', and '''k''' are each unit vectors because their magnitudes are each one. To make a vector of unit length, the vector must merely be divided by it's magnitude. | |||
Let v be a vector and u be the direction (unit vector) of v. | |||
v = <1,7,1> | |||
|v| = √(1<sup>2</sup> + 7<sup>2</sup> + 1<sup>2</sup>) = √51 | |||
u = v/|v| = <1/√51,7/√51,1/√51> | |||
Graalscript has a built-in function, '''vectornormalize({{graycourier|1=v}})''',to perform such a calculation. | |||
== Vector Modification == | == Vector Modification == | ||
| Line 30: | Line 40: | ||
=== Vector-Scalar Multiplication === | === Vector-Scalar Multiplication === | ||
[[Image:Vectors-scalar-multiplication.png|thumb|left|Vector-scalar multiplication]] | |||
With a vector, v, and a scalar, s, we could make a new vector that is s times larger than v. This can be accomplished in GraalScript with the function '''vectorscale({{graycourier|v}},{{graycourier|s}})'''. The vector is thus extended in the following manner: <br /> | With a vector, v, and a scalar, s, we could make a new vector that is s times larger than v. This can be accomplished in GraalScript with the function '''vectorscale({{graycourier|v}},{{graycourier|s}})'''. The vector is thus extended in the following manner: <br /> | ||
s·v = s·<v<sub>1</sub>,v<sub>2</sub>,v<sub>3</sub>> = <s·v<sub>1</sub>,s·v<sub>2</sub>,s·v<sub>3</sub>>. | s·v = s·<v<sub>1</sub>,v<sub>2</sub>,v<sub>3</sub>> = <s·v<sub>1</sub>,s·v<sub>2</sub>,s·v<sub>3</sub>>. | ||
<br clear="all" /> | |||
=== Vector Subtraction === | === Vector Subtraction === | ||
| Line 37: | Line 49: | ||
With these two properties, we find that vector subtraction is possible, and no longer a new idea. This is done in GraalScript with the use of the '''vectorsub({{graycourier|u}},{{graycourier|v}})''' function. <br /> | With these two properties, we find that vector subtraction is possible, and no longer a new idea. This is done in GraalScript with the use of the '''vectorsub({{graycourier|u}},{{graycourier|v}})''' function. <br /> | ||
u-v = u + (-v) = u + (-1)·v | u-v = u + (-v) = u + (-1)·v | ||
You can imagine this as the two | You can imagine this as the two vectors placed tip-to-end, but the second is facing the opposite direction. | ||
<br clear="all" /> | <br clear="all" /> | ||
=== Distance Between Terminal Points === | |||
Without creating a third vector, it is simple in GraalScript to find the distance between the two points at which two vectors end. This function is '''vectordist({{graycourier|u}},{{graycourier|v}})'''. <br /> | |||
The return value would be | |||
√((u<sub>1</sub>-v<sub>1</sub>)<sup>2</sup>+(u<sub>2</sub>-v<sub>2</sub>)<sup>2</sup>+(u<sub>3</sub>-v<sub>3</sub>)<sup>2</sup>) | |||
The mathematical operation is the pythagorean theorem (or a combination of two). As may be evident, the distance is the magnitude of '''u'''-'''v'''. | |||
== Other functions == | == Other functions == | ||
vectordot({{graycourier|u}},{{graycourier|v}}): see [[Dot Product]].<br /> | vectordot({{graycourier|u}},{{graycourier|v}}): see [[Dot Product]].<br /> | ||
vectorcross({{graycourier|u}},{{graycourier|v}}): see [[Cross Product]]. | vectorcross({{graycourier|u}},{{graycourier|v}}): see [[Cross Product]]. | ||
Latest revision as of 20:40, 5 April 2010
Vectors are mathematical representations of any thing that has a length, or magnitude, and direction. Positions are also described using vectors which start at the origin of the coordinate system (0,0,0).
Definition
In GraalScript, a vector is limited to three dimensions, however, mathematics allows for analyses of vectors in n-dimensions. Vectors do not have positions. Two vectors are said to be parallel if they have the same direction (u || v), and are said to be equal if they are parallel and have the same magnitude (u = v). Vectors are generally described by their terminal points with respect to the origin (0,0,0).
The basic format of a vector in GraalScript is {x,y,z} where x, y, and z are all floating points in reference to the axis to which they correspond. Built into GraalScript are several functions which can be used to analyze these vectors.
In mathematics, vectors are often written
v = <v1,v2,v3>
for a vector in three dimensions. They can also be written as the sum of unit vectors, i = <1,0,0>, j = <0,1,0>, and k = <0,0,1> on the x, y, and z axes, respectively. In this case, the vector would be written as
v = v1i + v2j + v3k
where the values of v are treated as scalars (numerical multipliers) of the unit vectors.
To denote the difference between a scalar and a vector, vectors are often written with a directional arrow above them, which looks like the top half of an arrow pointing right. In GraalScript, a scalar and a vector are impossible to confuse: a scalar is a floating point whereas a vector is a string.
Vector Length (Magnitude/Modulus)
Being as vectors are merely written by terminal point coordinates, there is no immediate way to determine the magnitude of the vector. Mathematically, the terminal point lies on a sphere that has the same radius as the vector's magnitude. Thus, we can use the equation of a sphere to calculate the magnitude.
r2 = x2 + y2 + z2
r = √(x2 + y2 + z2)
where r is the magnitude. Generally, the magnitude is denoted as |v| or ||v||. This was chosen, because absolute value refers to distance from the origin, thus the marks were suitable. In GraalScript, however, the magnitude of any vector can be calculated simply by plugging a vector string into the vectorlen(v) function.
Unit Length
A vector is said to have "unit length" when it's magnitude is one. i, j, and k are each unit vectors because their magnitudes are each one. To make a vector of unit length, the vector must merely be divided by it's magnitude. Let v be a vector and u be the direction (unit vector) of v.
v = <1,7,1> |v| = √(12 + 72 + 12) = √51 u = v/|v| = <1/√51,7/√51,1/√51>
Graalscript has a built-in function, vectornormalize(v),to perform such a calculation.
Vector Modification
Along with vectorlen are a plethora of functions built into GraalScript all for the purpose of modifying vectors.
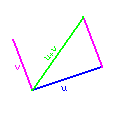
Vector Addition
Given the vectors u and v, we could create a third vector that has the magnitude of u and v, were the two vectors to be placed tip-to-end. This is called vector addition and can be done with the function vectoradd(u,v). This takes the terminal coordinates and adds them together. to make a new vector:
w = <u1+v1, u2+v2, u3+v3>.
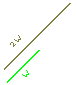
Vector-Scalar Multiplication
With a vector, v, and a scalar, s, we could make a new vector that is s times larger than v. This can be accomplished in GraalScript with the function vectorscale(v,s). The vector is thus extended in the following manner:
s·v = s·<v1,v2,v3> = <s·v1,s·v2,s·v3>.
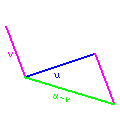
Vector Subtraction
With these two properties, we find that vector subtraction is possible, and no longer a new idea. This is done in GraalScript with the use of the vectorsub(u,v) function.
u-v = u + (-v) = u + (-1)·v
You can imagine this as the two vectors placed tip-to-end, but the second is facing the opposite direction.
Distance Between Terminal Points
Without creating a third vector, it is simple in GraalScript to find the distance between the two points at which two vectors end. This function is vectordist(u,v).
The return value would be
√((u1-v1)2+(u2-v2)2+(u3-v3)2)
The mathematical operation is the pythagorean theorem (or a combination of two). As may be evident, the distance is the magnitude of u-v.
Other functions
vectordot(u,v): see Dot Product.
vectorcross(u,v): see Cross Product.